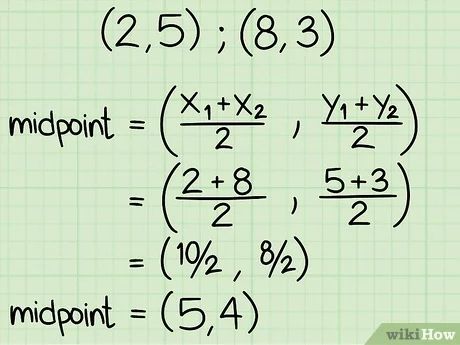
A perpendicular bisector is a line segment that is perpendicular to another line segment and passes through its midpoint. In geometry, it is often used to construct angles, triangles, and circles. Learning how to find the perpendicular bisector of two points is an essential skill in mathematics. In this article, we will discuss three different ways to find the perpendicular bisector of two points.

1. Algebraic Method:

The algebraic method involves finding the midpoint of the given line segment and determining the slope of a new line, which would be perpendicular to it. Follow these steps:

a) Calculate the midpoint (M) of the line segment defined by points A(x₁, y₁) and B(x₂, y₂):

M((x₁ + x₂)/2, (y₁ + y₂)/2)

b) Find the slope (m₁) of the line segment between A and B:

m₁ = (y₂ – y₁) / (x₂ – x₁)

c) Determine the negative reciprocal slope (-1/m₁), which will be the slope (m₂) of our perpendicular bisector.

d) Use point-slope form to calculate the equation of the perpendicular bisector passing through point M:

y – M(y) = m₂(x – M(x))

2. Geometric Method using a Compass:

This method requires a compass and straight edge (ruler). Follow these steps:

a) Place your compass at point A and draw an arc with a radius larger than half the length of your line segment.

b) Without changing the compass radius, place your compass at point B and draw another arc intersecting with the previous one.

c) Use your straight edge to draw a line through these two intersection points.

d) The resulting line will be your perpendicular bisector.

3. Using Technology or Specialized Software:

Modern technology offers an efficient method to find the perpendicular bisector of two points. There is a variety of online tools, software programs, or calculators available to help with geometric constructions:

a) Input the coordinates of two points (A and B).

b) Select the construction operation for a perpendicular bisector.

c) Follow any instructions or prompts given by the software, and it will generate the equation or visual representation of the perpendicular bisector.

In conclusion, understanding how to find the perpendicular bisector of two points can help you solve many geometric problems. Whether you choose to use algebraic methods, geometric constructions with a compass and straight edge, or utilize modern technology in specialized software or calculators, mastering this skill will not only benefit your mathematical journey but also broaden your problem-solving abilities.