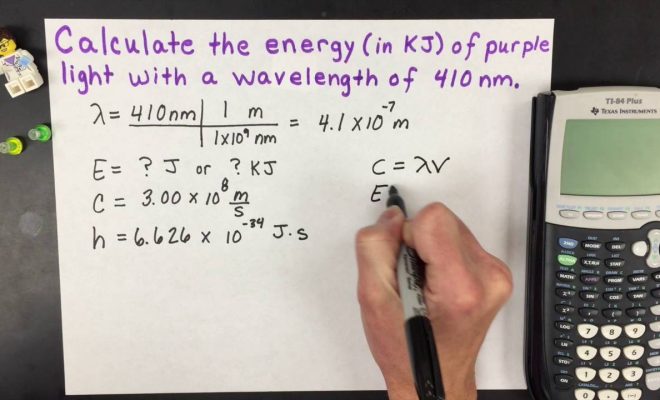
Light travels in the form of waves, and its energy can be calculated by analyzing its wavelength. Understanding how to calculate energy from wavelength allows us to analyze the behavior of light and better understand the physical world around us. In this article, we will explore the relationship between energy and wavelength, then provide a step-by-step guide on how to calculate energy from a given wavelength.

The Relationship between Energy and Wavelength:

The energy (E) of a photon, which is a discrete bundle of electromagnetic radiation, is inversely proportional to its wavelength (λ). This means that as the wavelength decreases, the energy of the photon increases and vice versa. The relationship between energy and wavelength is represented by Planck’s equation:

E = h * c / λ

where:

– E is the energy of the photon (measured in joules)

– h is Planck’s constant (6.626 x 10^-34 Js)

– c is the speed of light (3 x 10^8 m/s)

– λ is the wavelength of light (measured in meters)

Step-by-Step Guide to Calculating Energy from Wavelength:

1. Convert the wavelength to meters: To ensure compatibility with Planck’s equation, first convert your wavelength value into meters. For example: if your given wavelength is in nanometers, divide it by 10^9 to obtain its equivalent value in meters.

2. Calculate the product of Planck’s constant and the speed of light: Multiply Planck’s constant (6.626 x 10^-34 Js) by the speed of light (3 x 10^8 m/s) to obtain their product.

3. Divide this product by your converted wavelength value: Dividing this result by your converted wavelength value will yield the calculated energy for that specific wavelength.

4. Express your final answer in joules (J): As energy is measured in joules, ensure that your final answer is expressed in this unit.

Example calculation:

Given a wavelength of 450 nm, let’s calculate the energy of a photon with this wavelength.

1. Convert the wavelength to meters:

450 nm = 450 x 10^-9 m = 4.50 x 10^-7 m

2. Calculate the product of Planck’s constant and the speed of light:

(6.626 x 10^-34 Js) x (3 x 10^8 m/s) = 1.988 x 10^-25 Jm

3. Divide this product by your converted wavelength value:

(1.988 x 10^-25 Jm) / (4.50 x 10^-7 m) = 4.418 x 10^-19 J

4. Express your final answer in joules (J):

The energy of a photon with a wavelength of 450 nm is approximately 4.418 x 10^-19 J.

Conclusion:

By understanding the relationship between energy and wavelength, as well as how to apply Planck’s equation, you can calculate the energy of a photon from its given wavelength. With this knowledge at hand, you can better comprehend the behavior and properties of light in both scientific and everyday contexts.