The concept of derivatives is a fundamental building block in calculus and an essential tool for mathematicians, scientists, and engineers. By understanding how to calculate derivatives, you’ll uncover the hidden relationships between functions and their rates of change. In this article, we’ll explore the basic rules and techniques for finding derivatives of various functions.

1. Understanding the Concept of a Derivative:

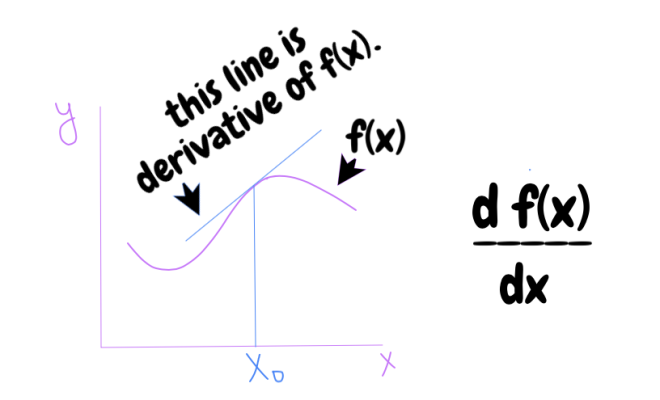
A derivative represents the rate of change of a function with respect to one of its variables. It provides information regarding how a function’s output changes as its input changes. In simple terms, it can be thought of as a measure of the slope or steepness of a function at any given point.

2. Basic Rules for Finding Derivatives:

Several basic rules can be applied to calculate derivatives. The most fundamental ones include:

a) Power Rule: If f(x) = x^n where n is a constant, then f'(x) = nx^(n-1)

b) Sum Rule: If f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x)

c) Difference Rule: If f(x) = g(x) – h(x), then f'(x) = g'(x) – h'(x)

d) Product Rule: If f(x) = g(x)*h(x), then f'(x) = g'(x)*h(x) + g(x)*h'(x)

e) Quotient Rule: If f(x) = g(x)/h(x), then f'(x) = (g'(x)*h(x)-g(x)*h'(x))/[h(x)]^2

f) Chain Rule: If f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x)

3. Higher Order Derivatives:

In many cases, you may need to find the second or higher-order derivatives – the rate at which the first derivative is changing. You can find the second derivative by taking the derivative of the first derivative and so on.

4. Applying Differentiation Techniques:

To become proficient in finding derivatives, you’ll need to practice applying these rules to various functions such as polynomial functions, trigonometric functions, exponential functions, logarithmic functions, and more. Remember that each function type may have specific rules or techniques for finding their derivatives.

Conclusion:

Understanding how to calculate derivatives is an important skill for those interested in mathematics and its applications. By mastering basic derivation rules and practicing them on different types of functions, you can effectively analyze problems related to rates of change and help make predictions in various fields like physics, engineering, economics, and much more.