The world of mathematics is vast and complex, with numbers playing a central role in our lives. Decomposing numbers – breaking them down into smaller, more manageable components – is a fundamental skill that can improve our understanding of arithmetic operations and help solve problems more efficiently. In this article, we will explore three techniques for decomposing numbers: using place value, utilizing number bonds, and applying prime factorization.

1.Place Value Decomposition

Place value decomposition is a basic yet powerful tool for breaking down numbers based on their position within the number itself. Each digit represents a different place value (ones, tens, hundreds, etc.) and can be written as a sum of its parts.

For example, consider the number 435:

435 = (4 × 100) + (3 × 10) + (5 × 1)

= 400 + 30 + 5

In this case, we have broken down the number into its hundreds, tens, and ones components.

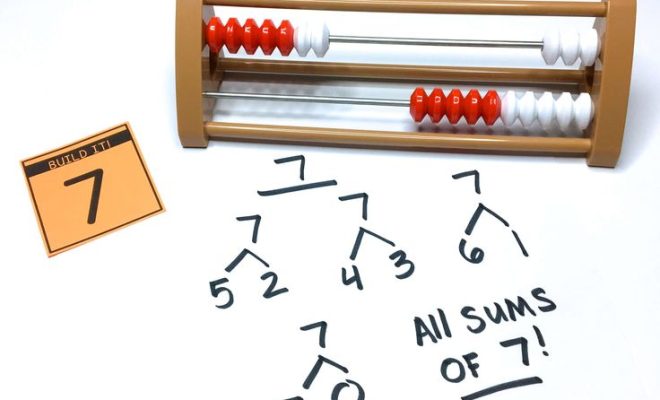
2.Number Bonds

Number bonds are a versatile method to decompose numbers by identifying different pairs or groups of smaller numbers that add up to the original number. This technique develops mental arithmetic skills and an understanding of how different combinations of numbers relate to one another.

For example, let’s look at the number 12:

_ Possible number bonds include:

– 12 = 1+11

– 12 = 2+10

– 12 = 3+9

– 12 = 4+8

– 12 = 6+6

You can use number bonds to split large numbers into two or more smaller numbers that are easier to work with in mathematical problems.

3.Prime Factorization

Prime factorization is a method for decomposing larger numbers into their prime factors – that is, the prime numbers that multiply together to reach the original number. This strategy exposes the underlying building blocks of composite (non-prime) numbers and can be particularly useful when tackling problems involving divisibility, greatest common divisors, or least common multiples.

For example, find the prime factorization of 56:

_ Start by dividing 56 by the smallest prime number (2):

56 ÷ 2 = 28

_ Divide the result by the smallest prime number again:

28 ÷ 2 = 14

_ Continue dividing:

14 ÷ 2 = 7

_ Since seven is a prime number, we have found all the prime factors:

56 = (2 × 2) × (2 × 7)

= (2³) × (7¹)

In conclusion, decomposing numbers using place value, number bonds, and prime factorization is an important skill to build a strong foundation in mathematics. These techniques can simplify complex problems and deepen your understanding of how numbers interact in various mathematical operations. So, implement these methods the next time you face a challenging numerical problem, and unlock your full potential in mathematics.